Лаборатория обратных задач естествознания

Ведётся разработка и апробация численных алгоритмов решения обратных задач для гиперболических уравнений, возникающих при решении задач сейсмики, акустики, теории упругости. Рассматриваемые математические модели соответствуют задачам определения параметров среды по результатам измерения отражённых волн на дневной поверхности. Разрабатываются методы решения, основанные на сведении задачи к системам линейных интегральных уравнений и их последующем решении (подход И.М. Гельфанда – Б.М. Левитана – М.Г. Крейна).

Разрабатываются методы решения задач по определению акустических параметров среды по конечному набору данных, измеряемых в фиксированных точках. Такие задачи возникают при моделировании процессов ультразвуковой томографии и связаны с определением параметров (плотность, скорость распространения волн, коэффициент поглощения) некоторых включений (моделирующих злокачественные образования в теле) в зондируемом объекте. Проводятся исследования эффективности и устойчивости алгоритмов, анализ влияния зондирующего импульса.

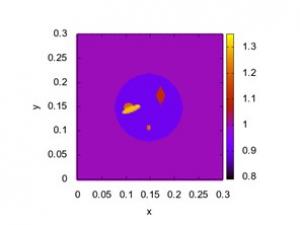
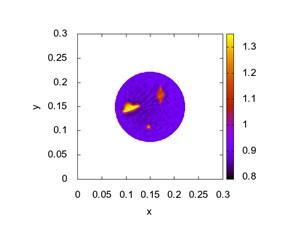
На рисунке 1 приведен пример восстановления акустических параметров фантома (результаты определения плотности). Слева – точная структура, справа –результат восстановления для системы из 16 источников и приёмников. Характерный размер наибольшего включения – 3 см, наименьшего – 0.5 мм.

Разрабатываются регуляризирующие алгоритмы численного решения и анализа прямых и обратных задач для математических моделей эпидемиологии (туберкулеза, ВИЧ, COVID-19, гепатита, гриппа), иммунологии (ВИЧ, злокачественных образований), экономики, социальных процессов (распространения информации в онлайн социальных сетях). Математические модели описываются системами обыкновенных дифференциальных уравнений, уравнений в частных производных, стохастических дифференциальных уравнений, случайными графами (агентные модели), коэффициенты и начальные условия которых могут быть заданы неизвестны. Разрабатываются методы анализа чувствительности и идентифицируемости исследуемых математических моделей.

На примере распространения новой коронавирусной инфекции в Новосибирской области построена агентно-ориентированная модель, в которой уточнены методами глобальной оптимизации параметры контагиозности вируса, тестирования, количества бессимптомных больных и др. по дополнительным измерениям о количестве выявленных случаев COVID-19 и проведенных тестов в регионе. В результате работы алгоритма построены сценарии развития распространения заболевания в регионе в зависимости от введенных карантинных мер. На рисунке 1 приведен сценарий распространения эпидемии в Новосибирской области с 01.11 по 16.12 на основе статистических данных с 16.03 по 31.10 в предположении отсутствия введения дополнительных карантинных мер.

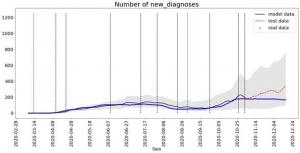
На рисунке 2 представлен результат моделирования количества ежедневно диагностируемых случаев (черная сплошная линия) до 01.11.2020 с дальнейшим прогнозом до 16.12.2020 (красная пунктирная линия). Синие точки - реальные данные (стопкоронавирус.рф), вертикальные черные линии - карантинные меры в регионе. Доверительный интервал построен по 10 запускам модели. Зелеными вертикальными пунктирными линиями обозначены дни, когда открывались и закрывались школы.