Лаборатория математического моделирования гидродинамических процессов в природной среде

И. о. завлабораторией д.ф.-м.н. Алексей Владимирович Пененко, эл. адрес: aleks@ommgp.sscc.ru. В составе лаборатории 4 кандидата и 3 доктора наук.

Тематика: разработка численных методов, математических моделей и алгоритмов для решения задач прямого и обратного моделирования гидротермодинамики, переноса и трансформации загрязняющих примесей в атмосфере и водных объектах, включая оз. Байкал. Разработка алгоритмов обработки изображений – спутниковых снимков и данных томографических исследований.

В лаборатории развивается концепция природоохранного прогнозирования и проектирования, основанная на методах совместного использования математических моделей и данных наблюдений характеристик изменения качества атмосферы и воды. Модели гидродинамики, переноса и трансформации загрязняющих примесей рассматриваются в предположении, что в самих моделях и во входных данных содержатся неопределенности, обусловленные различными факторами. Ключевыми элементами служат оценки функций чувствительности и неопределенности, участвующие в алгоритмах уточнения параметров моделей и содержащие информацию о степени адекватности результатов прогнозирования. Большое внимание в лаборатории уделяется методам усвоения данных, позволяющим в реальном времени учитывать в моделях данные различного характера: точечные, площадные, типа изображений. Предложены алгоритмы оценки качества систем мониторинга природных объектов. Разработаны эффективные методы восстановления внутренней структуры объектов для перспективных томографических сканеров.

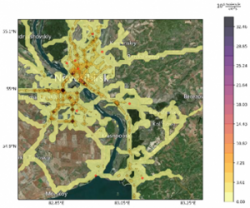
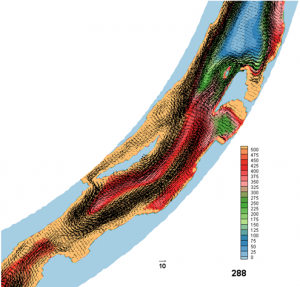
На примерах сибирских городов (Новосибирск, Красноярск, Чита) и городов Казахстана (Усть-Каменогрск, Алматы) изучались мезоклиматы и качество атмосферы городов и прилегающих регионов. Разработаны алгоритмы расчета полей концентраций многокомпонентных примесей и идентификации источников их эмиссий (рис. 1).

Рис. 1 – Результаты идентификации источников по данным мониторинга уровня загрязнения на 9 постах ГМС в Новосибирске с помощью алгоритма на основе оператора чувствительности (справа); заданное множество линейных источников (дорожная сеть города) (слева)

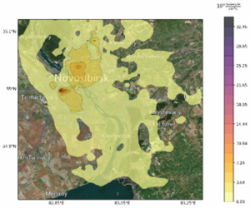
 Особое внимание в наших исследованиях уделяется Байкальскому региону и оз. Байкал. Моделирование распространения дымов от лесных пожаров и загрязняющих примесей от действующих на берегах предприятий – типичные задачи природоохранной тематики, равно как и поиск неизвестных источников загрязнений на основе данных наблюдений, полученных во время измерительных кампаний. В 2020–2023 гг. коллектив лаборатории выполнял работы по крупному проекту "Фундаментальные основы, методы и технологии цифрового мониторинга и прогнозирования экологической обстановки Байкальской природной территории" (рис. 2).

Рис. 2 – Рассчитанное поле ветра на высоте 100 м над поверхностью и контуры общей (вертикально интегрированной) концентрации в условных единицах: 5 час. по местному времени (29 час. с начала расчета) (слева); 12 час. дня по местному времени (через 36 час. модельного времени) (справа). Рассчитанные поля наложены на спутниковое изображение за 21.08.2015 (https://worldview.earthdata.nasa.gov )

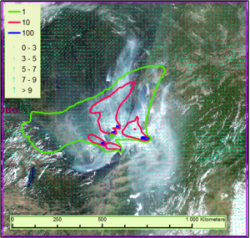
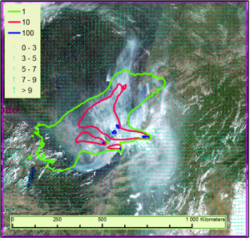
Решены фундаментальные задачи, важные для понимания физических процессов, идущих в оз. Байкал. Так, численные эксперименты показали, что одной из возможных причин глубокой конвекции, приводящей к обновлению вод до самых больших глубин, может быть всплытие твердых частиц (гидрата метана) в типичных зимних условиях стратифицированной водной толщи глубокого озера. По нашей гипотезе это же явление могло быть источником появления огромных кругов во льду оз. Байкал, замеченных космонавтами. Распространение нетипичной для озера водоросли спирогира явилось причиной беспокойства как местных жителей, так и научного сообщества. Ее появление связывают с антропогенным загрязнением, а за распространение отвечают гидродинамические процессы. Для оценки рисков загрязнения воды в озере рассмотрены гипотетические сценарии развития туризма. Распространение микропластика в водах озера в последнее время также привлекает всеобщее внимание (рис. 3).

Рис. 3 – Гипотетический наихудший сценарий возможного загрязнения в результате развития туризма на Байкале. Фрагмент сценария, относящийся к середине "климатического" сентября. Поле течений (см/сек) и концентрации примеси (усл. ед.) вблизи поверхности

С помощью трехпараметрической RANS-модели турбулентности исследовалась динамика устойчиво стратифицированного пограничного слоя атмосферы, которая характеризуется сложностью и наличием неустойчивости Кельвина - Гельмгольца, внутренних гравитационных волн, струй низкого уровня и других явлений.

В рамках Федеральных космических программ России на 2006–2025 гг. разработаны программные комплексы моделирования и валидации измерений бортовой аппаратуры перспективных отечественных космических аппаратов, программный комплекс обработки данных дистанционного зондирования Земли из космоса. Это программное обеспечение используется в оперативной и исследовательской работе центров приема и обработки спутниковых данных НИЦ "Планета" Росгидромета, а также при исследовании фотосферы Солнца в Научно-исследовательском институте ядерной физики МГУ. Разработаны превосходящие мировые аналоги алгоритмы для задач обнаружения объектов на изображениях. Работа коллектива отмечена наградами Федерации космонавтики России: д.ф.-м.н. В. П. Пяткин – орденом Ю. А. Гагарина и медалью им. акад. М. В. Келдыша, к.т.н. Салов Г. И. – медалью им. К. Э. Циолковского, к.т.н. А. А. Бучнев – почетным званием "Заслуженный испытатель космической техники".

Наиболее значимые публикации:

1. Penenko A.; Rusin E. Parallel implementation of a sensitivity operator-based source identification algorithm for distributed memory computers // Mathematics. 2022. No. 10. 4522. https://doi.org/10.3390/math10234522.

2. Kazantsev I. G., Turebekov R. Z. Sultanov, M. A. Inpainting of regular textures using ridge functions // Journal of Inverse and Ill-posed Problems. 2022. Vol. 30, No 5. P. 759–766. https://doi.org/10.1515/jiip-2021-0053.

3. Tsvetova E. Transport model: microplastic in Lake Baikal // Proc. SPIE. Vol. 12341. 28th Intern. Symp. on Atmospheric and Ocean Optics: Atmospheric Physics. 2022. 1234165. https://doi.org/10.1117/12.2644796.

4. Zubairova U. S., Kravtsova A. Yu., Romashchenko A. V., Pushkareva A. A., Doroshkov A. V. Particle-based imaging tools revealing water flows in maize nodal vascular plexus // Plants. 2022. Vol. 11, iss. 12. 1533. DOI: 10.3390/plants11121533.

5. Kazantsev I. G., Turebekov, R. Z., Sultanov, M. A. Restoration of images corrupted by stripe interference using Radon domain filtering // Sib. Electron. Math. Rep. 2022. Vol. 19, No. 2. P. 540–547. DOI: https://doi.org/10.33048/semi.2022.19.045.

6. Yarovenko I. P., Kazantsev I. G. An extrapolation method for improving the linearity of CT-values in X-ray pulsed tomography // Far Eastern Math. J. 2022. V. 22, No. 2. P. 269–275. https://doi.org/10.47910/FEMJ202238.

7. Методы математического моделирования для цифрового мониторинга и прогнозирования экологической обстановки // Фундаментальные основы, методы и технологии цифрового мониторинга и прогнозирования экологической обстановки Байкальской природной территории. Сер.: Интеграционные проекты СО РАН / Пененко А. В., Рапута В. Ф., Огородников В. А., Пененко В. В., Акентьева М. С., Амикишиева Р. А., Гочаков А. В., Каргаполова Н. А., Леженин А. А., Пьянова Э. А., Скорик В. С. Новосибирск: Изд-во СО РАН, 2022. С. 294–333.

8. Penenko A., Penenko V., Tsvetova E., Gochakov A., Pyanova E., Konopleva V. Sensitivity operator framework for analyzing heterogeneous air quality monitoring systems // Atmosphere. 2021. Vol. 12. No. 12.

9. Penenko A. Convergence analysis of the adjoint ensemble method in inverse source problems for advection-diffusion-reaction models with image-type measurements // Inverse Problems and Imaging. 2020. Vol. 14, No. 5. P. 757–782.

10. Getling A. V., Buchnev, A. A. The origin and early evolution of a bipolar magnetic region in the Solar photosphere // Astrophysical Journal. 2019. Vol. 871, No. 2. P. 224.

11. Penenko V. V., Penenko A. V., Tsvetova E. A., Gochakov A. V. Methods for studying the sensitivity of air quality models and inverse problems of geophysical hydrothermodynamics // JAMT. 2019. Vol. 60, No. 2. P. 392–399. DOI:10.1134/S0021894419020202.

12. Penenko A. A Newton – Kantorovich method in inverse source problems for production-destruction models with time series-type measurement data // Numerical Analysis and Applications. 2019. Vol. 12. P. 51–69 DOI:10.1134/S1995423919010051.

13. Penenko A. V.; Khassenova Z. T., Penenko V. V., Pyanova E. A. Numerical study of a direct variational data assimilation algorithm in Almaty city conditions // Eurasian Journal of Mathematical and Computer Applications. 2019. Vol. 7. P. 53–64. DOI:10.32523/2306-6172-2019-7-1-53-64.

14. Курбацкий А. Ф., Курбацкая Л. И. Исследование устойчивого пограничного слоя c использованием явной алгебраической модели турбулентности // Теплофизика и аэромеханика. 2019. Т. 26, № 3. С. 363–380.

15. Асмус В. В., Бучнев А. А., Кровотынцев В. А., Пяткин В. П., Салов Г. И. Комплекс программного обеспечения PlanetaMonitoring в прикладных задачах дистанционного зондирования // Автометрия. 2018. Т. 54, № 3. С. 7–23.

16. Kazantsev I. G., Olsen U. L., Poulsen H. F., Hansen P. C. A spectral geometric model for Compton single scatter in PET based on the single scatter simulation approximation // Inverse Problems. 2018. Vol. 34, No. 2. Paper 024002. DOI: 10.1088/1361-6420/aaa05d.

17. Granin N. G., Mizandrontsev I. B, Kozlov V. V., Tsvetova E. A., Gnatovskii R. Yu, Blinov V. V., Aslamov I. A., Kucher K. M., Ivanov V. G., Zhdanov A. A. Natural ring structures on the Baikal ice cover: analysis of experimental data and mathematical modeling // Russian Geology and Geophysics. 2018. Vol. 59, No. 11. P. 1514–1525, DOI: 10.1016/j.rgg.2018.10.011.

18. Kurbatskii A. F., urbatskaya L. I. Study of the neutral Ekman flow using an algebraic Reynolds stress model // Izvestiya, Atmospheric and Oceanic Physics. 2018. Vol. 54, No. 4. P. 336–343. DOI: 10.1134/S0002351518040119.

19. Салов Г. И. Обнаружение малоразмерных объектов на зашумленных изображениях при неизвестных вероятностных распределениях // Автометрия. 2018. Т. 54, № 5. С. 12–24.

20. Асмус В. В., Тимофеев Ю. М., Поляков А. В., Успенский А. Б., Головин Ю. М., Завелевич Ф. С., Козлов Д. А., Рублев А. Н., Кухарский А. В., Пяткин В. П., Русин Е. В. Температурное зондирование атмосферы по данным спутникового ИК Фурье-спектрометра // Известия РАН. Физика атмосферы и океана. 2017. Т. 53, № 4. С. 487–492.

21. Гранин Н. Г., Козлов В. В., Цветова Е. А., Гнатовский Р. Ю. Полевые исследования и некоторые результаты численного моделирования кольцевой структуры на льду озера Байкал // Доклады РАН. 2015. Т. 461, № 3. С. 343.

22. Пененко В. В., Цветова Е. А., Пененко А. В. Методы совместного использования моделей и данных наблюдений в рамках вариационного подхода для прогнозирования погоды и качества состава атмосферы // Метеорология и гидрология. 2015. № 6. С. 13–24. (23 цитирования).

23. Penenko V. V., Tsvetova E. A., Penenko A. V. Variational approach and Euler's integrating factors for environmental studies // Computers & Mathematics with Applications. 2014. Vol. 67, No. 12. P. 2240–2256. (42 цитирования)

24. Penenko V., Baklanov A., Tsvetova E., Mahura A. Direct and inverse problems in a variational concept of environmental modeling // Pure Appl. Geophys. 2012. Vol. 169. P. 447–465. DOI: 10.1007/s00024-011-0380-5.